1.4: Rotation Matrices and Orthogonal Matrices

Jeffrey R. Chasnov
Hong Kong University of Science and Technology

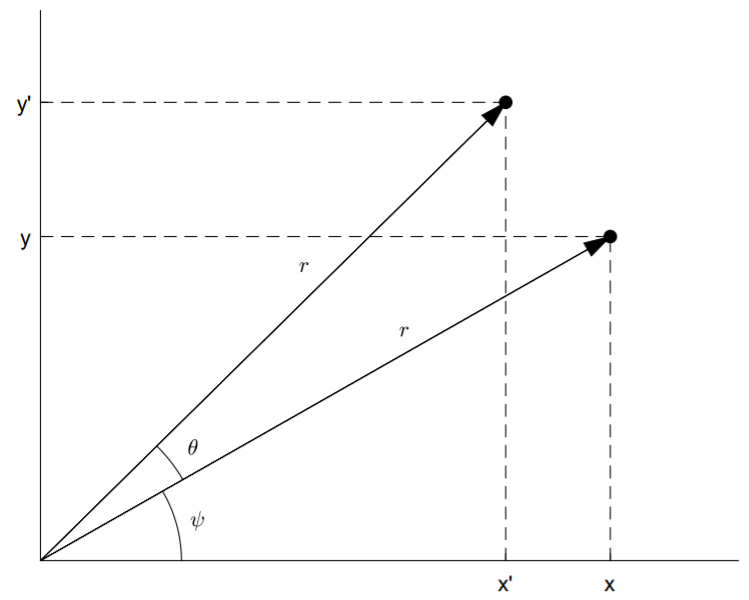
$clipboard_e15cdc6c9afba1f7599a072c24a3b5498.png$

View Rotation Matrix on YouTube View Orthogonal Matrices on YouTube Consider the two-by-two rotation matrix that rotates a vector through an angle $θ$ in the $x$-$y$ plane, shown above. Trigonometry and the addition formula for cosine and sine results in \[\begin x'&=r\cos(\theta+\psi) \\ &=r(\cos\theta\cos\psi -\sin\theta\sin\psi )\\&=x\cos\theta-y\sin\theta \\ y'&=r\sin(\theta+\psi)\\&=r(\sin\theta\cos\psi+\cos\theta\sin\psi) \\ &=x\sin\theta+y\cos\theta.\end \nonumber \] Writing the equations for $x'$ and $y'$ in matrix form, we have \[\left(\beginx'\\y'\end\right)=\left(\begin\cos\theta&-\sin\theta \\ \sin\theta&\cos\theta\end\right)\left(\beginx\\y\end\right).\nonumber \] The above two-by-two matrix is called a rotation matrix and is given by \[\text_\theta =\left(\begin\cos\theta&-\sin\theta \\ \sin\theta&\cos\theta\end\right).\nonumber \]

Example $\PageIndex$

Find the inverse of the rotation matrix $\text_\theta$. Solution The inverse of $\text_θ$ rotates a vector clockwise by $θ$. To find $\text^_θ$, we need only change $θ → −θ$: \[\text_\theta^=\text_=\left(\begin\cos\theta&\sin\theta \\ -\sin\theta&\cos\theta\end\right).\nonumber \] This result agrees with (1.4.4) since $\det\text< R>_\theta =1$.

Notice that $\text^_θ = \text^>_θ$. In general, a square $n$-by-$n$ matrix $\text$ with real entries that satisfies \[\text^=\text^>\nonumber \] is called an orthogonal matrix. Since $\text^> = \text$ and $\text^>\text = \text$, and since $\text^>$ multiplies the rows of $\text$ against themselves, and $\text^>\text$ multiplies the columns of $\text$ against themselves, both the rows of $\text$ and the columns of $\text$ must form an orthonormal set of vectors (normalized and mutually orthogonal). For example, the column vectors of $\text$, given by \[\left(\begin\cos\theta \\ \sin\theta\end\right),\quad\left(\begin-\sin\theta \\ \cos\theta\end\right),\nonumber \] are orthonormal. It is clear that rotating a vector around the origin doesn’t change its length. More generally, orthogonal matrices preserve inner products. To prove, let $\text$ be an orthogonal matrix and $x$ a column vector. Then \[(\text)^>(\text)=\text^>\text^>\text=\text^>\text.\nonumber \] The complex matrix analogue of an orthogonal matrix is a unitary matrix $\text$. Here, the relationship is \[\text^=\text^\dagger .\nonumber \] Like Hermitian matrices, unitary matrices also play a fundamental role in quantum physics.

This page titled 1.4: Rotation Matrices and Orthogonal Matrices is shared under a CC BY 3.0 license and was authored, remixed, and/or curated by Jeffrey R. Chasnov via source content that was edited to the style and standards of the LibreTexts platform.

Back to top
- 1.3: The Identity Matrix and the Zero Matrix
- 1.6: Matrix Representation of Complex Numbers

Was this article helpful?
Yes
No

1.4: Rotation Matrices and Orthogonal Matrices

Example \(\PageIndex\)

Recommended articles